odop
Open Design Optimization Platform (ODOP) - Coil spring design app; mechanical springs; compression spring, extension spring, torsion spring
Terminology
The following terms have special meanings used in the context of this program. The terms appear in an order ranked from more general and introductory to more specific.
On this page:
- MATHEMATICAL MODEL
- DESIGN TYPES
- INDEPENDENT VARIABLES
- DEPENDENT VARIABLES
- CALCULATION INPUTS
- CONSTRAINTS
- CONSTRAINT VIOLATIONS
- FUNCTION CONSTRAINTS (FDCL)
- FIX
- AUTO FIX
- AUTO SEARCH
- FEASIBLE REGION
- OBJECTIVE FUNCTION
- PREFERENCES
- PROPERTIES
- EQUATION SETS
- SEARCH
- SEEK
- TRADE
- ODOP DESIGN LIBRARY
- MIGRATION
- ALERTS
- VALIDITY
- SPRING DESIGN VARIABLE NAMES
- FACTOR OF SAFETY
MATHEMATICAL MODEL
A mathematical model is a set of equations that describes the behavior of a real world problem of interest. Within the context of the ODOP software, the terms "mathematical model", "design type" and "equation set" are closely related. Each design type has a mathematical model at its core.
For examples, see:
Common numerical issues associated with mathematical models
A general mathematical model with no limits or loose limits to its inputs will contain vulnerabilities to undesired behavior created by "pathological" cases. Common examples are divide-by-zero and square root of a negative number. These situations create singularities in the design space. With ODOP, there are cases where a search will fail to find the correct result because a singularity lies between the search start point and a known good solution.
Spring Design Example
The analysis of round wire helical coil springs provides an example for the case where coil outside diameter (OD_Free) is exactly twice the wire diameter (Wire_Dia). In this situation, the inside diameter (ID_Free) is exactly zero and the spring index (Spring_Index) is exactly one. That value of Spring_Index results in a divide-by-zero problem in the calculation of the Wahl curvature correction factor (kc). Javascript renders the result as infinity which then propagates through dependent equations. Eventually, equations involving operations like subtraction of infinities create values of NaN which propagate to additional dependent equations.
See also:
DESIGN TYPES
A Design Type is a specific design problem. As noted above, each Design Type has a mathematical model of some aspect of the real world at its core. Examples included with the ODOP software include compression, extension and torsion springs, a Rectangular Solid and a Piston-Cylinder. A "design" is a specific and unique instance of a Design Type. These designs can be opened, edited and saved in a way similar to the way that word processing documents, spreadsheets and graphic presentations operate. The ODOP software stores multiple designs of each Design Type in its database (a.k.a. design library).
INDEPENDENT VARIABLES (inputs, design parameters)
The independent variables are the inputs of the design equations. They are the quantities on the right hand side of the equals sign that can be arbitrarily selected by the designer or search algorithm. Once values are selected for all independent variables, the design is completely determined.
In engineering design optimization, independent variables are the quantities that are changed by the designer in order to optimize the design. Dependent variables are the quantities that are affected by the independent variables. The goal of optimization is to find the optimal values of the independent variables that result in the best performance of the dependent variables
The set of independent variables for the current design are easily identifiable in Advanced View.
Look in the upper left under the heading "Independent Variable (IV)".
For example, independent variables for the Rectangular Solid sample problem appear as:
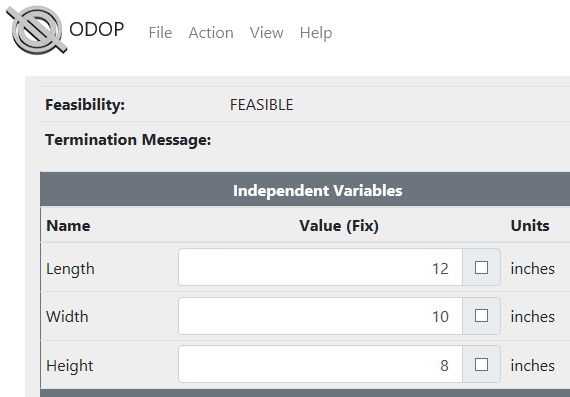 In the Calculator View of spring design,
Independent Variables are a white entry field without an asterisk in the upper left.
In the Calculator View of spring design,
Independent Variables are a white entry field without an asterisk in the upper left.
For independent variables, a Fixed status reduces the computational demand of the numerical search problem. See the Fix entry below for more details.
DEPENDENT VARIABLES (outputs, state variables)
The dependent variables are the outputs of the design equations. They are the quantities on the left hand side of the equal sign. Frequently, dependent variables are measures of the performance of a given design and can be thought of as indicating the "state" of the design. A Search is required to establish appropriate values of the independent variables to produce the desired values of dependent variables. The desired values are expressed by constraints and Fixed status.
In engineering design optimization, dependent variables are the quantities that are affected by the independent variables. The goal of optimization is to find the optimal values of the independent variables that result in the best performance of the dependent variables .
The set of dependent variables for the current design are easily identifiable in Advanced View.
Look in the mid left under the heading "Dependent Variable (DV)".
For example, dependent variables for the Rectangular Solid sample problem appear as:
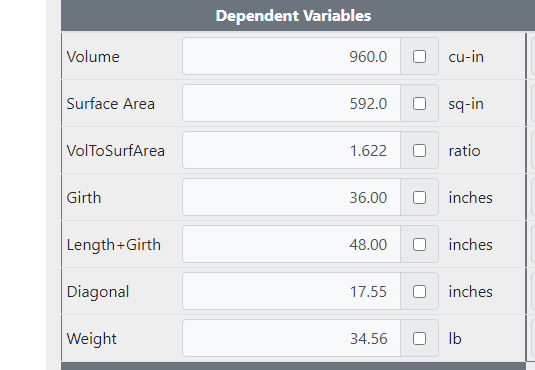
In the Calculator View of spring design,
Dependent Variables are a white entry field with an asterisk in the upper left.
A dependent variable in Fixed status increases the computational demand of the numerical search problem. See the FIX entry below for more details.
CALCULATION INPUTS (other inputs)
Calculation Inputs are inputs to the design equations and are adjustable by the user, but are not manipulated by the search algorithm or subject to Fix or constraints. Calculation Inputs frequently represent material properties or other physical parameters.
CONSTRAINTS
Constraints are one sided boundaries that represent goals for the design problem. Either dependent or independent variables may be constrained to be greater than or less than a simple constant or a functionally determined quantity such as a different dependent or independent variable or Calculation Input. The section below on FUNCTION CONSTRAINTS provides more information on this subject.
In order to establish a constraint, it is necessary to check the corresponding Minimum or Maximum constraint checkbox and enter a value for the desired constraint level in the corresponding entry field.
If any constraint is violated, a Search operation is required to establish appropriate values of the free (not Fix status) Independent Variables to meet the specified constraint levels. In order to save time and provide more predictable operation, ODOP will stop the search process if it gets very close to a feasible design but still violates one or more constraints by a fraction of a percent. In this case, the design is referred to as "feasible" or "marginally feasible" as opposed to "strictly feasible".
Design Situations provides more insights on how constraints are used to properly specify a design problem.
CONSTRAINT VIOLATIONS
A constraint violation represents the difference between the current value of a given variable and its corresponding constraint level. By convention, negative values represent constraint satisfaction, positive values represent constraint violation.
FUNCTION CONSTRAINTS (FDCL)
When a constraint level is determined as the value of another Independent Variable, Dependent Variable or Calculation Input (as opposed to being a simple constant), it is referred to as a "Functionally Determined Constraint Level" (FDCL). Such constraint levels can be configured by selecting (clicking into) the (MIN or MAX) constraint value field of eligible variables. After clicking a constraint field of an eligible variable, the user will be able to select from a list of variable names available to be used as constraint levels. The variables that can be constrained this way and the variables that are eligible as choices to be selected as constraints are configured in the design type's initialState.
More specific information is available in the On-line Help section covering extension spring constraints.
FIX and FREE
The user can establish (i.e. Fix or hold) the value of any variable, independent or dependent. Fix status is designated by checking the checkbox immediately to the right of the variable's value.
Placing an Independent Variable in Fix status simply removes that variable from the set that is manipulated by the Search algorithm. This reduces the computational effort required for the Search to find a solution. The user can change the value of an Independent Variable by entering a different value in that variable's value field. The corresponding values of dependent variables are calculated and displayed immediately.
Fixing a Dependent Variable is accomplished internally by establishing a weighted, double-sided constraint. While not a significant concern, this increases the computational effort required for the Search to find a solution. Once the appropriate Fix checkbox is checked, enter a target value in either the Minimum or Maximum constraint level entry field. A Search (Action : Search menu) is required to establish the desired values.
Clearing the checkbox (Free status) allows the Search to alter the value of the corresponding variable subject to constraints, if established.
A "design" is determined primarily (ignoring the role of Calculation Inputs for the moment) by the set of independent variables. While a variable in Fix status cannot have its value adjusted in order to contribute to achieving a feasible design, Search will adjust the value of other variables in Free status to achieve feasibility. If no variables with Free status are available, Search will produce an error message.
Establishing additional constraints and placing variables in Fix status can reduce the ability of Search to find a feasible solution. Too many constraints and variables in Fix status can create an over-specified situation.
See also:
AUTO FIX
Enabled by default, the Auto Fix feature automatically applies "Fixed" status to Independent Variables changed by user entry.
See: Auto Fix for details.
See also:
AUTO SEARCH
Enabled by default, the Auto Search feature automatically triggers a Search operation after user input.
See: Auto Search for details.
See also:
FEASIBLE REGION
A feasible region may be formed within the boundaries represented by the various constraints on the design problem. If a given design satisfies all the constraints, it is said to be "feasible" or in the "feasible region". If the constraint levels are set such that the constraints overlap, no solution that satisfies the design equations and the constraints simultaneously can be found. The search will terminate with multiple constraints violated. In this case, there is no feasible region.
When faced with the situation where no feasible solution is available, the designer must restructure the problem or his goals in some way to permit the desired solution. Perhaps the solution is to use a stronger material. This can be represented by changing a material constant and re-executing the search. Perhaps use of the TRADE feature is appropriate. For more information, see: Trade.
OBJECTIVE FUNCTION
The objective function constitutes the numerical search problem. It is formed as a blend of violated constraints, dependent variable Fix violations and in the case of the SEEK feature, a "merit function" that represents the variable under investigation. The search algorithm works to drive the objective function to the lowest value possible. For more detail, see the SEARCH entry below.
PREFERENCES
(Internal Control Settings File : Preferences menu item)
Preference settings control the operation of the program. They have no direct meaning to the design problem. For more specific information, refer to the documentation section (on-line Help entry) on Search and Tutorial session tutor9.
PROPERTIES
(File : Properties menu item)
It is possible to store a series of text strings with a design in order to carry descriptive information. The File : Properties menu is used to establish a set of label - value pairs where the text of the value is set by the user.
For coil spring designs, the content of these fields is displayed on Report 3. Thus, information entered into File : Properties can be used to support the documentation of a spring design. See your browser documentation for details on how to print or save into .PDF format a page like Report 3. From there, the information can be included as part of a Request for Quotation or other transfer of the design information.
The number of labels and the text of the label are established in the design type source code in the initialState.js file.
See also:
EQUATION SETS
The ODOP software allows for multiple design types and thus multiple sets of design equations (mathematical models of a specific design problem) to be concurrently available. Currently implemented Design Types include:
The simplest way to use a different design type and equation set is to select a design type that uses the desired equation set at the time that the ODOP software first starts. A default design named "Startup" should be available for each design type. An explanation of how to select a design type and open a design of that type is provided in: Getting Started.
Additional information on how to implement new ODOP design types is available in the NewDesignType documentation.
SEARCH
The term "Search" is used in the sense of "Search for a solution". The ODOP Search feature (Action : Search menu item or Search button) is used to find a feasible design. As a manual operation used to find a solution, Search is conceptually similar to a manual recalculation operation in a spreadsheet program.
Search stops when it finds the first feasible design. In order to optimize a design, see Seek below.
See also:
SEEK
The Seek feature (Action : Seek menu item or Seek button) will automatically invoke Search to maximize or minimize the target variable subject to the prevailing constraints and FIXes.
For example in spring design, a designer might want to seek designs providing maximum cycle life or minimum weight.
See also:
TRADE
The Trade feature (Action : Trade menu item) is used when a feasible solution is not available. TRADE provides decision support for relaxation of constraints by guiding the designer to restructure his goals in a way that is most consistent with the original objectives.
Trade will automatically invoke Search to help locate the "nearest" feasible point when a feasible solution is not available with the existing set of constraints. "Nearest" in this case means the feasible point reached with the least total relaxation of constraints.
For example in spring design, if constraints representing objectives for both weight and cycle life are violated, the designer could ask Trade to find the first (nearest) feasible design that relaxes only the weight constraint, only the cycle life constraint or some weighted combination of the two.
See also:
ODOP DESIGN LIBRARY
The design library is a database physically located on an Internet server, a.k.a. "in the cloud". Design information stored in the design library does not appear on the local storage of your computer. You must be logged in to an ODOP user account in order to save designs into the ODOP design library.
See: User Accounts for details on how to obtain an ODOP user account.
MIGRATION
The term "migration" refers to the process of upgrading designs created in a previous version of the software to the format required by the current version. This process changes the underlying data structures that describe the design. Opening a design saved in a prior version will produce a pop-up message of the form:
"Migrated design from version {previous version number} to {current version number}".
Saving the design will eliminate the message on future open operations. Complete detail on the latest changes is available in GitHub.
The Help : About menu item lists the Design Model version for the currently open design type in the form: "Design Model version {current version number}".
Help : About also displays the current ODOP software version in the form: "Software version {Major.Minor.Patch}". The ODOP version is independent of the version of any specific design type (a.k.a. model). A change in software version may or may not be associated with a change in the design model version number for any design type. A change in the version number of any design type will usually be associated with a change in the minor or major field of the ODOP software version.
ALERTS
Alerts are informational messages that are produced as you change the values of your design.
See also:
VALIDITY
Designs with values outside their valid range are likely physically impossible. In spring design, negative values for wire diameter, coil diameter and number of coils are obvious examples. Other situations, for example where an increase in wire diameter results in a negative value for coil inside diameter or where an increase in force at the second load point takes a compression spring below its solid condition may be a bit less obvious.
Each design type has a starting point, a.k.a. initialState, that contains minimum and maximum valid values for each variable. More specifically, Independent Variables, Dependent Variables and numeric Calculation Inputs all have pre-assigned ValidMin and ValidMax values. These validity ranges are used to generate Alerts and also guide the Search process toward valid results.
See also:
SPRING DESIGN VARIABLE NAMES
Variable names illustrated on compression spring Force-Deflection diagram:
See also:
FACTOR OF SAFETY
This term is described in detail in the spring design overview section: Factor of Safety
See also:
- Wikipedia - Factor of Safety
- Terms common to all spring types
- Compression spring
- Extension spring
- Torsion spring